My childhood hero from the 1970s was the Six Million Dollar Man. Equipped with his superior bionic eye, he easily outwitted the villains as they stumbled through their evil plots using only their limited, natural vision. I reminisce about this TV character every year when I show a lecture theatre full of undergraduates the first slide in my “Physics of Light and Vision” course, which shows a face with cameras staring out of the eye sockets. I then invite my students to debate the pros and cons of artificial vision.

Technological advances over the past few decades have transformed this debate from the wild speculations of science fiction into the practicalities of science fact. For one thing, the number of photodiodes that capture light in digital cameras has escalated, driven by an exponential growth of “pixels per dollar”. Furthermore, surgeons can now insert electronic chips into the retina. The grand hope is to restore vision by replacing damaged rods and cones with artificial photoreceptors – and clinical trials to show this are already under way.

The striking similarities between the eye and the digital camera help towards this endeavour. The front end of both systems consists of an adjustable aperture within a compound lens, and advances bring these similarities closer each year. It works both ways. On the one hand, for example, some camera lenses now feature graded refractive indices similar to the eye’s lens. On the other, a laser-surgery technique called Lasik removes aberrations from the surface of the eye’s cornea (which acts as the first lens in the eye’s compound-lens system) in order to resemble the shape found in camera lenses. Meanwhile, a quick glance at the back of a camera shows that it is getting closer to the eye’s retina in terms of both the number of light-sensitive detectors and the space that they occupy. A human retina typically contains 127 million photoreceptors spread over an area of 1100 mm². In comparison, today’s state-of-the-art CMOS sensors feature 16.6 million photoreceptors over an area of 1600 mm².

However, there are crucial differences between how the human visual system and the camera “see”, both in the physical structure of the detectors and the motions they follow. For example, the neurons in the eye responsible for transporting electrical information from the photoreceptors to the optic nerve have a branched, fractal structure, whereas cameras use wires that follow smooth, straight lines. And while a camera captures its entire field of view in uniform detail – recording the same level of information at the centre of the image as at the edges – the eye sees best what is directly in front and not so well at the periphery. To allow for this, the eye constantly moves around, exploring one feature at a time for a few moments before glancing elsewhere at another, in a gaze pattern that is fractal; whereas the camera’s gaze is static with a pattern that is described by a simple dot.

The differences between camera technology and the human eye arise because, while the camera uses the Euclidean shapes favoured by engineers, the eye exploits the fractal geometry that is ubiquitous throughout nature. Euclidean geometry consists of smooth shapes described by familiar integer dimensions, such as dots, lines and squares. The patterns traced out by the camera’s wiring and motion are based on the simplicity of such shapes – in particular, one-dimensional lines and zero-dimensional dots, respectively. But the eye’s equivalent patterns instead exhibit the rich complexity of fractal geometry, which is quantified, as we will see, by fractional dimensions. It is important that we bear in mind these subtleties of the human eye when developing retinal implants, and understand why we cannot simply incorporate camera technology directly into the eye. Remarkably, implants based purely on camera designs might allow blind people to see, but they might only see a world devoid of stress-reducing beauty.

More than meets the eye

Early theories of human senses highlighted some of the unique qualities of the eye. The “detectors” associated with hearing, smelling, tasting and touching are all passive. They gather information that arrives at the body. For example, the ear and nose wait for sound waves and airborne particles to arrive before they respond. Consequently, the early Greek philosophers of the atomist school proposed an equally passive theory of human vision in which the eye collected and detected “eidola” – a mysterious substance that all objects shed continually.

Unfortunately, although the concept of eidola provided an appealing theory for human vision, it triggered an avalanche of scientific problems in terms of the world being viewed. For example, let us say I receive eidola from the Cascade Mountains seen from my office window in Oregon. Would the mountains not wear down, given that they must emit enough eidola for the other million people who also view the Cascades on a daily basis?

Luckily, optical theories emerged to save the atomists from their increasingly contrived models of the material world and gradually progressed towards the geometric optics that we enjoy today. But even the best optical theories suffered from a weakness: given that light rays bounce off a friend’s face, why can we not spot it immediately in a crowd – even though it is directly before our eyes? We are forced to conclude that the visual system is not passive but that it has to hunt for the information we need.

Hunting is a necessary strategy for the eye because the world relentlessly bombards us with visual stimuli. Our basic behaviour is composed of strategies aimed at coping with this visual deluge. For example, we walk round a corner at a distance that ensures that the scene emerges at a rate that we can process. However, our biggest strategy for coping lies in the way the photoreceptors are distributed across the retina and in the associated motion of our eyes.

If the eye employed the Euclidean design of cameras and distributed its photoreceptors in a uniform, 2D array across the retina, there would simply be too many pixels of visual information for the brain to process in real time. Instead, most of the eye’s seven million cones are piled into the central region of the retina. The cone density reaches 50 cones per 100 µm at the centre of the fovea, which is a pin-sized region positioned directly behind the eye lens. Unlike the camera’s passive collection of information, the eye instead has to move to ensure that the image of interest falls mainly on the fovea. Consequently, although the fovea comprises less than 1% of the retinal size, it uses more than 50% of the visual cortex of the brain.

We know a lot about how the eye moves in certain situations. If viewing a face, for example, we look first at the eyes and then the mouth. But little research has focused on how we search for information in a more complex scene. On reflection this seems to be an oversight, as the evolution of our visual system has been fuelled by natural scenery. Typical objects in these scenes each consist of structures that repeat at different magnifications. In other words, the complexity of what we have evolved to see is built up of self-similar, fractal objects such as plants, clouds and trees. How would we therefore search for something like a tiger hiding in a fractal forest?

Gazing patterns

To address the question of how we pick out the important bits of knowledge from the vast scene before our eyes, my collaborators Paul Van Donkelaar and Matt Fairbanks (also at the University of Oregon) and I used the remote-eye-tracking system shown in figure 1a, which uses an ordinary optical camera to track the position of a participant’s pupil. To detect where the participant is actually looking a beam of infrared light is shone onto the cornea and the position of the reflected ray is measured with a separate infrared camera. The participants spent time viewing a series of computer-generated fractal patterns (figure 1b). A computer algorithm then uses information from the cameras to calculate the participant’s gaze as a function of time and generates eye trajectories similar to that shown in figure 1c.

One of the intriguing properties of a fractal pattern is that its repeating structure causes it to occupy more space than a smooth 1D line, but not to the extent of completely filling the 2D plane. As a consequence, a fractal’s dimension, D, has a value lying between 1 and 2. By increasing the amount of fine structure in the fractal, it fills more of a 2D plane and its D value moves closer towards 2. We tweaked this parameter to generate various series of computer-generated fractal patterns, for which the dimension ranged from 1.1 to 1.9 in 0.1 intervals.

Our results showed that, when searching through the visual complexity of a fractal pattern, the eye searches one area with short steps before jumping a larger distance to another area, which it again searches with small steps, and so on, gradually covering a large area. This behaviour was observed throughout the D-value range from 1.1 to 1.9.

To quantify the gaze of the eye we again turned to fractals, as its trajectory is also like a fractal – a line that starts to occupy a 2D space because of its repeating structure. Simulated eye trajectories (figure 1d) demonstrate how gaze patterns with different dimensions would look. We employed the well-established “box counting” method to work out our values of D exactly. This involved covering each trajectory with a computer-generated mesh of identical squares (or “boxes”), and counting the number of squares, N(L), that contain part of the trajectory. This count is repeated as the size, L, of the squares is reduced. For fractal behaviour, N(L) scales according to the power law relationship N(L) ~ L^–D, where D lies between 1 and 2. Our results showed that, in every instance, the eye trajectories traced out fractal patterns with D = 1.5, which is what is simulated in the middle panel of figure 1d. The insensitivity of the eye’s observed pattern to the wide range of D values shown to subjects is striking. It suggests that the eye’s search mechanism follows an intrinsic mid-range D value when in search mode.

A possible explanation for this insensitivity lies in previous studies of the foraging behaviour of animals. These studies proposed that animals adopt fractal motions when searching for food. Within this foraging model, the shorter trajectories allow the animal to look for food in a local region and then increasingly long trajectories allow it to travel to unexplored neighbouring regions and then on to regions even further away. The interpretation of this behaviour is that, through evolution, animals have found it to be the most efficient way to search an area for food. Significantly, fractal motion (figure 1d, middle) has “enhanced diffusion” compared with Brownian motion (figure 1d, right), where the path mapped out is, instead, a series of short steps in random directions. This might explain why a fractal trajectory is adopted for both an animal’s searches for food and the eye’s search for visual information. The amount of space covered by fractal trajectories is larger than for random trajectories, and a mid-range D value appears to be optimal for covering terrain efficiently.

Fractal therapy

Our finding that the eye adopts an innate searching pattern raises an intriguing question: what happens when the eye views a fractal pattern of D = 1.5? Will this trigger a “resonance” when the eye sees a fractal pattern that matches its own inherent characteristics? My collaborations with psychologists and neuroscientists support this intriguing hypothesis. Perception experiments performed on hundreds of participants over the past decade show that mid-D fractals are judged to be the most aesthetically appealing, and physiological measures of stress (including skin conductance measurements and electro-encephalography (EEG)) reveal that exposure to these fractals can reduce our physiological response to stress by as much as 60%. Furthermore, preliminary functional-magnetic-resonance-imaging (fMRI) experiments indicate that mid-D fractals preferentially activate distinct regions of the brain. This includes the parahippocampal area, which is associated with the regulation of emotions such as happiness.

Each year, the UK and the US each spend an average of $1000 per capita on stress-related illnesses, and so increased exposure to computer-generated mid-D fractals could present a novel, non-pharmaceutical approach to reducing society’s stress levels by harnessing these positive physiological responses. The current strategy is to use computer-generated images both for viewing on computer monitors and also for printing out and hanging on walls. The advantage of using large flat-screen monitors is that we can generate time-varying fractals, which we believe will be important for maintaining people’s attention. We are also starting a project in which we will work with artists to incorporate stress-reducing fractals into their work. To “train” the artists, we hope to develop software that can give the fractal dimension of any piece of art, so that the artists can use these to see if they are hitting optimal D values.

Crucial to our stress levels, though, is our daily exposure to nature’s mid-D fractals such as clouds, trees and river patterns, which prevent our stress levels from soaring out of control. According to our model, the physiological origin of this stress reduction lies in the commensurability between the fractal eye motion and the fractal scene, which in turn results from the non-uniform distribution of cones across the retina.

Adapting technology, not adopting

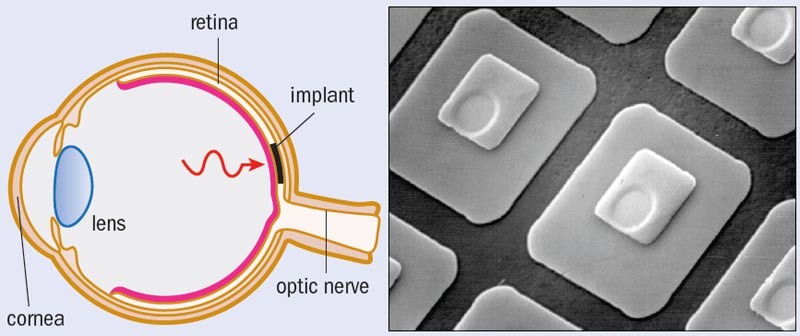
So what are the implications of the eye’s natural stress-reducing mechanism for retinal implants? Retinal diseases such as macular degeneration cause the rods and cones in the retina to deteriorate and lose functionality. Implants are inserted into the damaged region of the retina to replace damaged photoreceptors (figure 2). Referred to as “subretinal” implants, these state-of-the-art devices typically consist of a 3 mm semiconductor chip incorporating up to 5000 photodiodes. If we want to retain the stress-reduction mechanism, the distribution of photodiodes across the implant should mimic that of the retina. The point is that if the distribution were even, the eye would no longer need to move and so it would learn not to, and this lack of motion would prevent the stress reduction from kicking in. Unfortunately, current implant designs do simply feature the uniform distribution of photodiodes found in the passive camera. This discrepancy will have a growing impact as future chips replace increasingly large regions of the retina.

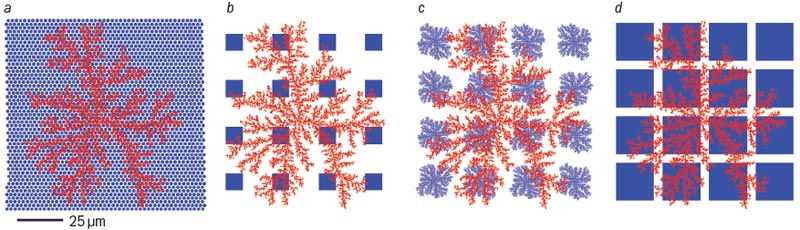
This flaw emphasizes the subtleties of the human visual system and the potential downfalls of adopting, rather than adapting, camera technology for eye implants. A similar downfall would result from assuming that the implant’s photodiodes should be connected to the retina using the Euclidean-shaped electrodes found in cameras. Figure 3 shows different patterns of “wiring” and how these interface with a retinal neuron. Although macular degeneration damages rods and cones, it leaves the retinal neurons intact and so these can be used to connect an implant’s photodiode electrodes to the optic nerve. Part a shows healthy photoreceptors, while parts b–d show a series of different shapes of electrodes that could be used in implants.

Retinal neurons are fractal in structure, and the simulated version in figure 3 characterized by D = 1.7 closely resembles the image of a real retinal neuron shown in figure 4a. If yield is defined as the percentage of electrodes that overlap with, and therefore establish electrical contact to, a neuron, then current retinal implants (figure 3b) have a yield of 81%.

Although this yield is greater than the 46% for the configuration in figure 3a, retinal implants do not match the performance of healthy human eyes. The artificial retina would still underperform compared with a healthy retina, as healthy retinas have a higher density of photoreceptors. The number of photoreceptors connected in figure 3a is 1050, compared with only 13 photodiodes in figure 3b. Artificial retinas must therefore be somehow brought up to speed.

One way to achieve this is to increase the yield beyond 81% for artificial retinas. Figure 3c shows the 94% yield achieved by replacing the square-shaped Euclidean electrodes with fractal electrodes. This yield increase could also be achieved by using larger square electrodes, as shown in figure 3d. However, this strategy would fail to take into account another striking difference between the camera and the eye. A camera manufacturer would never feed the wiring in front of the photoreceptors because it might hinder the passage of light to them. Yet this is exactly what happens in the eye. The layer of retinal “wiring” sits in front of the rods and cones, which means that light has to pass through this to reach the photoreceptors. As a consequence, the implant electrodes also have to sit in front of the photodiodes if they are to connect to the retinal neurons. The increased area of electrodes in figure 3d would therefore prevent the light from reaching the implant’s photodiodes.

In contrast, the fractal electrodes of figure 3c allow both high connection yield and high transmission of light to the photodiodes. This property results from the branching that recurs at increasingly fine scales. The fractal branches spread across the retinal plane while allowing light to transmit though the gaps between the branches, and a high D value maximizes this effect. As noted earlier, retinal neurons have a D value of 1.7.

Artificial neurons

Rick Montgomery (also at the University of Oregon) and I, in collaboration with Simon Brown at the University of Canterbury, New Zealand, employ a technique called nanocluster deposition to construct fractal electrodes with the aim of establishing an enhanced connection between retinal implants and healthy retinal neurons. In the technique, nanoclusters of material are carried by a flow of inert gas until they strike a substrate, where they self-assemble into fractal structures using diffusion-limited aggregation. These so-called nanoflowers (figure 4b) are characterized by the same D value as the retinal neurons that they will attach to.

During the deposition process, the nanoflowers nucleate at points of roughness on the substrate. Therefore, when nanoflowers are grown on top of the implant’s photodiodes, the surface roughness will be exploited to “automatically” grow the nanoflowers, making this a highly practical process for future implants. One challenge of the growth process lies in reducing nanocluster migration along nanoflower edges, which smears out the fine branches. This can be achieved by tuning the cluster sizes (which range from several nanometres up to hundreds of nanometres) and adjusting their deposition rate.

The nanoflowers can be grown to match the size of the photodiodes (20 µm), and will feature branch sizes down to 100 nm. Many of the gaps between the fractal branches will therefore be smaller than the wavelength of visible light, opening up the possibility of using the physics of fractal plasmonics to “super lens” the electromagnetic radiation into the photodiodes.

Significantly, the inherent advantages of the nanoflower electrodes lie in adopting the fractal geometry of the human eye rather than the Euclidean geometry of today’s cameras. Although the superior performance of the Six Million Dollar Man’s bionic eye is still in the realm of science fiction, the road to its invention will inevitably feature many lessons from nature.

At a glance: Artificial vision

• Surgeons restore human vision by replacing diseased photoreceptors in the retina with semiconductor implants based on digital cameras
• The physical structure and motion of the retina are based on nature’s fractal geometry, in contrast to the Euclidean geometry used by photosensitive chips in digital cameras
• Nanocluster growth technology will be used to self-assemble artificial neurons on the surface of future retinal implants that mimic the fractal structure of the eye’s natural neurons
• Pattern analysis reveals that the eye searches for visual information using a fractal motion, similar to that of foraging animals, that covers an area more efficiently than random motion
• The spatial distribution of photoreceptors across an implant has to match that found in the eye in order to trigger a physiological stress-reducing mechanism associated with the eye moving its gaze to observe fractal scenes

More about: Artificial vision

E Cartlidge 2007 Vision on a chip Physics World March pp35–38
M S Fairbanks and R P Taylor 2010 Scaling analysis of spatial and temporal patterns: from the human eye to the foraging albatross Non-linear Dynamical Analysis for the Behavioral Sciences Using Real Data (ed) Stephen J Guastello and Robert A M Gregson (Boca Raton, CRC Press) pp341–366
S A Scott and S A Brown 2006 Three-dimensional growth characteristics of antimony aggregates on graphite Euro. Phys. J. D 39 433–438
R P Taylor et al. 2005 Perceptual and physiological responses to the visual complexity of fractals Nonlinear Dynamics, Psychology, and Life Sciences 9 89–114
G M Viswanathan et al. 1996 Lévy flight search patterns of wandering albatrosses Nature 381 413–415