Bose-Einstein condensation is an exotic quantum phenomenon that was observed in dilute atomic gases for the first time in 1995, and is now the subject of intense theoretical and experimental study
In 1924 the Indian physicist Satyendra Nath Bose sent Einstein a paper in which he derived the Planck law for black-body radiation by treating the photons as a gas of identical particles. Einstein generalized Bose’s theory to an ideal gas of identical atoms or molecules for which the number of particles is conserved and, in the same year, predicted that at sufficiently low temperatures the particles would become locked together in the lowest quantum state of the system. We now know that this phenomenon, called Bose-Einstein condensation (BEC), only happens for “bosons” – particles with a total spin that is an integer multiple of h, the Planck constant divided by 2 pi.
This Bose condensate, and the process of condensation itself, was predicted to have many unusual properties and for years experimenters have tried to produce Bose-Einstein condensation in the laboratory. Finally in 1995 groups at JILA, a laboratory run by the National Institute of Standards and Technology and theUniversity of Colorado in Boulder, Colorado, and the Massachusetts Institute of Technology (MIT) obtained compelling evidence for Bose-Einstein condensation in dilute atomic gases.
Both the Boulder and MIT groups, and a group at Rice University in Houston, Texas, have since improved the techniques for creating and observing this exotic quantum phenomenon, and rapid progress has been made in understanding its dynamic and thermodynamic properties. At MIT we have recently verified the intriguing feature that Bose-condensed atoms are “laser-like” – in other words, that the matter waves of the atoms are coherent. In these experiments we have succeeded in observing coherence directly, and have demonstrated a rudimentary “atom laser” that generates a beam of coherent atoms, in analogy to emission of coherent photons by an optical laser. At the same time, theorists have clarified many fundamental issues and have developed powerful methods to simulate real systems.
Order reigns in the ground state
The dynamical behaviour of a gas at room temperature is not affected by the fact that one atom cannot be distinguished from another. In accordance with the Heisenberg uncertainty principle, the position of an atom is smeared out over a distance given by the thermal de Broglie wavelength, lambdadB = (2 pi h-bar2 / kBmT)1/2, where kB is the Boltzmann constant, m is the atomic mass and T is the temperature of the gas. At room temperature the de Broglie wavelength is typically about ten thousand times smaller than the average spacing between the atoms. This means that the matter waves of the individual atoms are uncorrelated or “disordered”, and the gas can thus be described by classical Boltzmann statistics.
As the gas is cooled, however, the smearing increases, and eventually there is more than one atom in each cube of dimension lambdadB. The wavefunctions of adjacent atoms then “overlap”, causing the atoms to lose their identity, and the behaviour of the gas is now governed by quantum statistics.
Bose-Einstein statistics dramatically increase the chances of finding more than one atom in the same state, and we can think of the matter waves in a Bose gas as “oscillating in concert”. The result is Bose-Einstein condensation, a macroscopic occupation of the ground state of the gas. (In contrast, fermions – particles with a total spin of (n + ½)h, where n is an integer – cannot occupy the same quantum state.) Einstein described the process as condensation without interactions, making it an important paradigm of quantum statistical mechanics.
The density distribution of the condensate is represented by a single macroscopic wavefunction with a well defined amplitude and phase, just as for a classical field. Indeed, the transition from disordered to coherent matter waves can be compared to the change from incoherent to laser light.
Chilling the atoms
Bose-Einstein condensation has been cited as an important phenomenon in many areas of physics, but until recently the only evidence for condensation came from studies of superfluid liquid helium and excitons in semiconductors. In the case of liquid helium, however, the strong interactions that exist in a liquid qualitatively alter the nature of the transition. For this reason a long-standing goal in atomic physics has been to achieve BEC in a dilute atomic gas. The challenge was to cool the gases to temperatures around or below one microkelvin, while preventing the atoms from condensing into a solid or a liquid.
Efforts to Bose condense atoms began with hydrogen more than 15 years ago. In these experiments hydrogen atoms are first cooled in a dilution refrigerator, then trapped by a magnetic field and further cooled by evaporation (see below). This approach has come very close to observing BEC, but is limited by the recombination of individual atoms to form molecules and by the detection efficiency.
In the 1980s laser-based techniques such as Doppler cooling, polarization-gradient cooling and magneto-optical trapping were developed to cool and trap atoms. These techniques profoundly changed the nature of atomic physics and provided a new route to ultracold temperatures that does not involve cryogenics. Atoms at sub-millikelvin temperatures are now routinely used in a variety of experiments. Alkali atoms are well suited to laser-based methods because their optical transitions can be excited by available lasers and because they have a favourable internal energy-level structure for cooling to low temperatures.
However, the lowest temperature that these laser cooling techniques can reach is limited by the energy of a single photon. As a result, the “phase-space density” – the number of atoms within a volume lambdadB3 – is typically about a million times lower than is needed for BEC.
The successful route to BEC turned out to be a marriage of the cooling techniques developed for hydrogen and those for the alkalis: an alkali vapour is first laser cooled and then evaporatively cooled. In evaporative cooling, high-energy atoms are allowed to escape from the sample so that the average energy of the remaining atoms is reduced. Elastic collisions redistribute the energy among the atoms such that the velocity distribution reassumes a Maxwell-Boltzmann form, but at a lower temperature. This is the same evaporation process that happens when tea cools, but the extra trick for trapped atoms is that the threshold energy can be gradually lowered. This allows the atomic sample to be cooled by many orders of magnitude, with the only drawback being that the number of trapped atoms is reduced.
The challenge in combining these two cooling schemes for alkalis was a question of atomic density. Optical methods work best at low densities, where the laser light is not completely absorbed by the sample. Evaporation, on the other hand, requires high atomic densities to ensure rapid rethermalization and cooling. This changed the emphasis for optical methods: while they had previously been used to produce low temperatures and high phase-space density simultaneously, they now needed to produce high elastic collision rates. Furthermore, this had to be achieved in an ultrahigh vacuum chamber to prolong the lifetime of the trapped gas. Thus no new concept was needed to achieve BEC, but rather it was an experimental challenge to improve and optimize existing techniques. These developments were pursued mainly at MIT and Boulder from the early 1990s.
Improved techniques in magnetic trapping
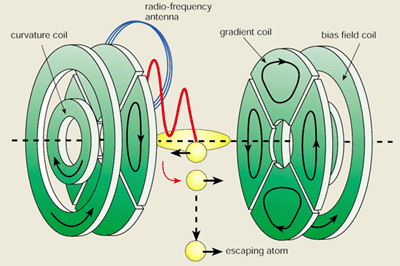
For evaporative cooling to work, the atoms must be thermally isolated from their surroundings. This must be done with electromagnetic fields, since at ultracold temperatures atoms stick to all surfaces. The best method for alkalis is magnetic confinement, which takes advantage of the magnetic moment of alkali atoms. After the atoms are trapped and cooled with lasers, all light is extinguished and a potential is built up around the atoms with an inhomogeneous magnetic field. This confines the atoms to a small region of space.
Atoms can only be cooled by evaporation if the time needed for rethermalization is much shorter than the lifetime of an atom in the trap. This requires a trap with tight confinement, since this allows high densities and hence fast rethermalization times. For this reason, the first experiments that observed BEC used so-called linear quadrupole traps, which have the steepest possible magnetic fields.
These techniques do indeed produce high densities and fast evaporation, but with one major problem: the magnetic field is zero at the centre, which causes an atom to become “disorientated” and lose the alignment of its magnetic moment. Since a magnetic field can only confine atoms with magnetic moments that are antiparallel to the field, these “spin flips” result in a disastrous loss of atoms from the trap. Both the Boulder and MIT groups found ways to circumvent this problem. The Boulder group added a rotating magnetic field to keep the atoms away from the “hole”, while we “plugged” the hole with the repulsive force from a focused laser beam.
Both of these schemes were successful but had major limitations. In March 1996 we observed BEC in a novel “cloverleaf” magnetic trap that overcame these limitations. This trap is a variant of the Ioffe-Pritchard trap, first suggested back in 1983, and has a non-zero magnetic field at its centre to avoid the loss of atoms. The confinement is tight in two directions and relatively weak in the third, which gives rise to cigar-shaped, rather than spherical, trapped clouds. The novelty of the trap lies in the “cloverleaf” winding pattern of the coils, which allows excellent optical access to the sample for laser cooling and trapping, and for probing the condensate (see figure 1). The design has proved to be reliable and versatile, and most of the experimental results described here were obtained with this trap. In view of the effort that has gone into designing traps in recent years, it is rather surprising that the most suitable configuration dates back over 13 years.
Evaporation can be readily achieved in a magnetic trap using electron spin resonance. The magnetic moments of trapped atoms are flipped by applying a radio-frequency field in resonance with the energy difference between the spin-up and spin-down states. The frequency of the field is adjusted so that it only affects the atoms at the edge of the cloud – in an harmonic oscillator potential, these atoms have the highest energy. When the moments of these atoms are flipped, the magnetic forces become anti-trapping and the atoms are expelled from the trap. As the cloud cools it shrinks towards the centre of the trap, so the frequency of the radio-frequency field must be continually reduced to maintain evaporation at the edge of the cloud.
In our experiments we start with sodium atoms effusing from an oven at a temperature of 600 K (a velocity of 800 m s-1) and a density of about 1014 cm-3. Over a distance of 0.5 m the atoms are first slowed with a laser beam to a speed of around 30 m s-1. This is slow enough for around 1010 atoms to be captured in a magneto-optical trap. Some tricks with laser cooling and trapping reduce the temperature of the gas to about 100 µK, which is cold enough for the atoms to be trapped with magnetic fields. Evaporation then cools the gas to about 2 µK – the temperature at which a condensate forms – in roughly 20 s.
Coincidentally, the density of atoms at condensation is about 1014 cm-3, similar to that in the atomic beam oven. Thus the cooling sequence lowers the temperature by 8 to 9 orders of magnitude. During evaporative cooling we typically lose a factor of 1000 atoms and form condensates with 107 atoms. In the cloverleaf trap the condensates can be up to 0.3 mm long. Condensation has thus provided us with macroscopic quantum objects.
Observing condensation
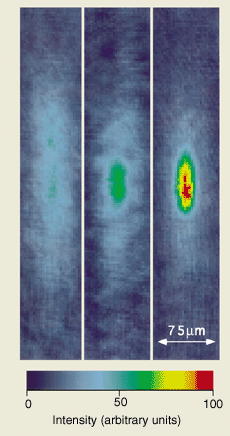
Trapped condensates are very small and optically thick, so they are difficult to observe in the trap. The first observations of BEC were made by switching the trap off and allowing the atoms to expand ballistically. A laser beam in resonance with an atomic transition was then flashed on, and the resulting absorption of light created a “shadow” that was recorded by a camera. This snapshot of atomic positions indicates how much the atoms have expanded since they were released from the trap, and hence it records their velocity distribution. The atoms in the condensate expand very little because they are in the lowest energy state, and the dramatic signature of Bose condensation was thus the sudden appearance of a sharp peak of atoms in the centre of the image.
Absorption imaging is inherently destructive because the atoms are released from the trap. Moreover, the absorbed photons also heat the atoms. In early 1996 we observed a Bose condensate non-destructively using “dark-ground” imaging, a technique that relies on dispersion rather than absorption.
Dispersion and absorption are conveniently described together by a complex index of refraction. The imaginary part of the index describes the absorption of photons from the probe beam, followed by inelastic scattering of the light through large angles. The real part corresponds to coherent elastic scattering through small angles. This dispersive scattering alters the phase of the light, and since the light is only slightly deflected, the technique is virtually non-perturbative. The key point is that if the probe laser is detuned sufficiently far from any atomic resonances, dispersive scattering dominates absorption and the condensate then simply looks like a piece of shaped glass – in other words like a lens.
To “see” the condensate using dispersive scattering, the phase shift introduced by the atoms must be transformed into a variation in intensity. This is a well known problem in optics and can be solved by spatial filtering. The signal in the Fourier plane is modified either with opaque objects (“dark-ground imaging”) or with phase-shifters (“phase-contrast imaging”).
The non-destructive nature of dispersive imaging allows many images to be taken of the same condensate. Figure 2 shows the formation of a condensate observed with phase-contrast imaging. Such real-time movies will be invaluable in studying the dynamical behaviour of a condensate.
Theory and first experiments
The theoretical study of trapped weakly interacting Bose gases has a long history, starting in the 1950s with the pioneering work of Gross and Pitaevskii on the macroscopic wavefunction for such systems. The past year has seen a dramatic increase in the number of papers devoted to the theory of trapped Bose gases, indicative of the many unsolved and intriguing questions that are attracting the interest of the scientific community.
Roughly speaking, there are two aspects to the theoretical research. On the one hand there is the solution of the “many-body problem” in the case of many atoms occupying the ground state. The challenge is to understand how the interatomic forces modify the structural properties of condensates such as ground state configuration, dynamics and thermodynamics. The second issue of great interest is the study of coherence and superfluid effects in these novel systems.
Theoretical studies of the structural properties have been stimulated by the recent availability of experimental data. For a dilute Bose gas, interaction effects are simplified by the fact that collisions take place only between pairs of atoms and can be described in terms of a single parameter, the s-wave scattering length (which in most cases is a distance comparable with the range of the interaction). This situation is in stark contrast to the complex interactions that exist in liquid helium.
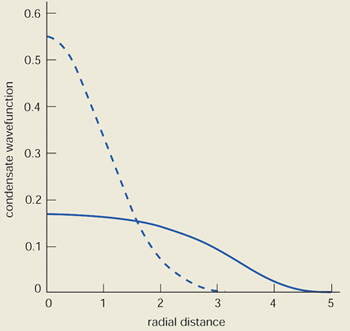
However, an important message emerging from the recent theoretical work is that two-body interatomic forces in condensates can be highly significant, even though the gas is dilute. In the Schrödinger equation for the condensate wavefunction, the significance of interactions depends on the size of the interaction energy per atom compared with the ground-state energy of the harmonic trap. This ratio is a function of Na/aHO, where a is the s-wave scattering length, aHO is the amplitude of oscillation of a particle in the ground state and N is the number of atoms. Although a/aHO is typically about 10-3, N can be ~ 107, so interactions can strongly modify the ground-state wavefunction and the ground-state energy (see figure 3). This predicted dependence of the energy on the number of atoms has been verified by experiments at both Boulder and MIT.
From the time-dependent Schrödinger equation it is possible to investigate the normal modes of oscillation of a Bose condensate. These are analogous to the phonon and roton excitations that have been extensively studied in superfluids. Historically, understanding collective quantum excitations has played a crucial role in explaining the properties of superfluid liquid helium and was the subject of pioneering work by Lev Landau, Nikolai Bogoliubov and Richard Feynman (see Donnelly in Further reading).
For a trapped Bose gas the equations of motion have a form that was derived by Bogoliubov in 1947, and recently these have been studied extensively. When the parameter Na/aHO is very large the equations take the simple form of the hydrodynamic equations for superfluids. For an isotropic harmonic-trapping potential the frequency, omega, of the quantum excitations is found to follow the dispersion law omega = omega0(2n2 + 2nl + 3n + l)1/2, where omega0 is the frequency of the trap, n is the number of nodes in the wavefunction along a radius of the trap and l is the angular momentum carried by the excitation. This should be compared with omega = omega0(2n + l) for particles that do not interact. The role of the interactions is particularly important in the “surface” modes (n = 0), where they reduce the energies of the excitations from omega = omega0l to omega = omega0l1/2.
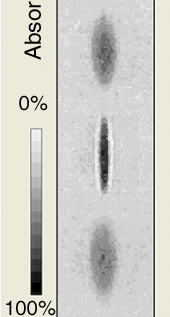
The hydrodynamic equations can also be solved analytically for anisotropic traps, and have provided useful predictions for the experiments at Boulder and MIT. In these experiments the condensates were gently “shaken” by modulating the magnetic trapping fields, inducing oscillations in the shape of the condensate. The mode shown in figure 4 is the analogy of a quadrupole oscillation for a cigar-shaped cloud: contraction along the long direction is accompanied by expansion along the short direction and vice versa. Experiments at MIT verified the theoretical prediction for the frequency of this mode to 1%. Indeed, the measurements of the internal energy and the frequency of collective excitations carried out at both Boulder and MIT have provided the most spectacular and convincing proof of the importance of interactions in condensates.
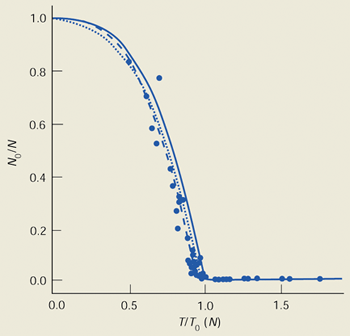
The effects of two-body interactions are less crucial when the temperature is increased towards the BEC transition temperature. This is because atoms become thermally excited and spread out to form a much more dilute gas than the condensate. Early measurements at MIT confirmed that the predictions for a non-interacting gas for the transition temperature kBT0 = 0.94h-bar omega0 N1/3 and for the “condensate fraction” – the proportion of atoms that are condensed – N0/N = 1 -(T/T0)3 are not strongly affected by interactions.
However, theory predicts that interactions should effect both T0 and N0/N, and it should be possible to observe these effects by measuring both quantities with high precision. At Boulder a shift of N0 consistent with theoretical expectation has been observed, but this shift is comparable to the uncertainty in the measurement (figure 5). In general, the thermodynamic behaviour of trapped Bose gases shows interesting differences compared to the uniform (constant density) case. In particular, interactions in a uniform gas raise T0, while for a trapped gas it is lowered.
Many theoretical questions for trapped Bose gases remain to be explored and understood. Two major issues concerning collective excitations are the treatment of oscillations near to T0 and the mechanisms by which oscillations are damped, particularly at low temperatures. Related questions concern nonlinear effects in excitations, the onset of chaotic phenomena and the variation of excitation frequencies with temperature.
An important problem is the behaviour of trapped gases with negative s-wave scattering lengths. In the experiments at MIT and Boulder the scattering lengths are positive. This means that the effect of the two-body collisions is to cause repulsion between the atoms (“hard-sphere” collisions), and in such an instance it is theoretically well understood that a Bose condensate is stable. For negative scattering lengths, however, the forces between the atoms are attractive and tend to cause a condensate to collapse. This is believed to prevent condensation completely in a uniform system and restrict the number of atoms that can be condensed in an inhomogeneous system such as a trap. Measurements of BEC in lithium have been carried out at Rice University and the number of condensed atoms is consistent with theory.
As mentioned above, the property of superfluidity (i.e. persistent flow without viscous damping) is closely related to the existence of long-range order, or coherence, in the ground state. Indeed, the superfluid velocity is proportional to the gradient of the phase of the ground-state wavefunction. This implies, for example, that the moment of inertia of a Bose gas below T0 differs from that expected for a rigid body. Superfluidity and coherence phenomena will become challenging areas for future research. Theorists have already made quantitative predictions for the Josephson-type effects and interference phenomena associated with the phase of the condensate wavefunction. The role of vortices in the dynamics of the system, the possible occurrence of “second sound”, and the interplay between collective excitations, rotational properties and superfluidity are further problems of fundamental interest.
Realization of a basic atom laser
The possibility of producing a coherent beam of atoms, which could be collimated to travel large distances or brought to a tiny focus like an optical laser, has sparked the imagination of atomic physicists. Such an atom laser could have a major impact on the fields of atom optics, atom lithography and precision measurements.
A Bose-Einstein condensate is a sample of coherent atomic matter and is thus a good starting point for an atom laser. The process of condensing atoms into the ground state of a magnetic trap is analogous to stimulated emission into a single mode of an optical laser and one can think of the trap as a resonator with “magnetic mirrors”. An important feature of a laser is an output coupler to extract a fraction of the coherent field in a controlled way, and at MIT we recently demonstrated such a device for a trapped Bose gas.
Since a magnetic trap can only confine atoms with magnetic moments lying antiparallel to the magnetic field, we altered the “reflectivity” of the magnetic mirrors by applying a short radio-frequency pulse to tilt the magnetic moments of the atoms. The atoms extracted in this way were accelerated under gravity and observed by absorption imaging. By changing the amplitude of the radio-frequency field, the extracted fraction could be varied between 0% and 100% (see Physics World 1996 October p18).
A crucial feature of a laser is the coherence of its output – in other words, the presence of a macroscopic wave. In theoretical treatments coherence has been used as the defining criterion for BEC. However, none of the measurements described so far have provided evidence for long-range order. For example, although measurements of the collective agree with the solutions of the Schrödinger equation at zero temperature, similar frequencies have been predicted for a classical gas in the hydrodynamic regime.
One method to investigate coherence is to look for the effects of the phase of the condensate wavefunction. In superconductors this phase has been observed through the Josephson effect, and in liquid helium it has been inferred from the motion of quantized vortices. The phase is a complex quantity, which means it can only be detected as an interference effect between two different wavefunctions, analogous to the interference between two independent laser beams. The subject of coherence and the interference properties of trapped Bose gases has recently received considerable theoretical attention. The under-lying theoretical questions are of major interest and concern. For example, does the concept of spontaneous symmetry breaking (an important concept throughout physics) apply in systems with small atom numbers, and what are the effects of the particle-particle interactions on the phase of the condensate (“phase diffusion”)?
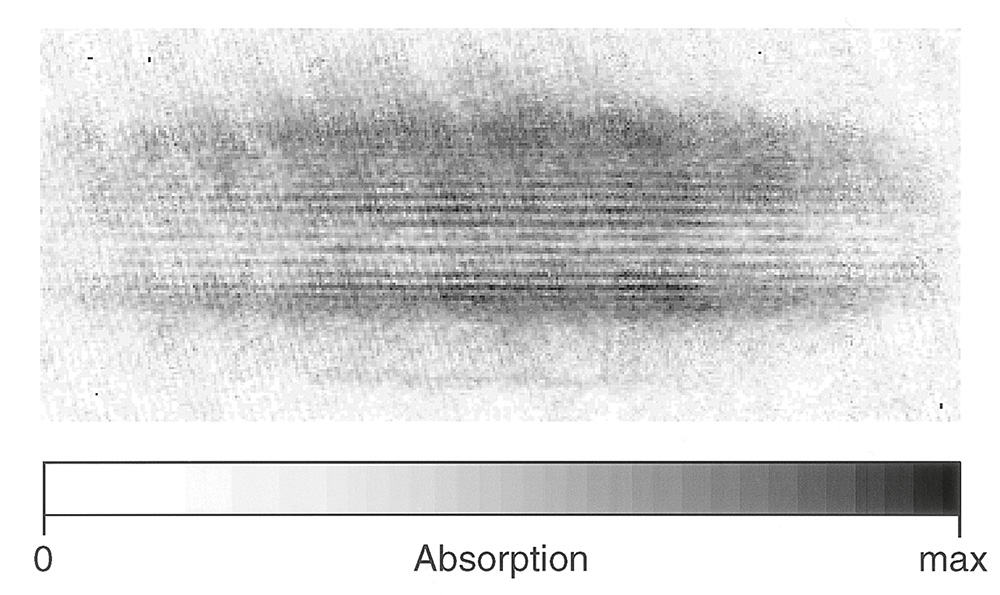
At MIT we have recently observed high-contrast interference of two independent Bose condensates, and thus showed that a condensate does indeed have a well defined phase. We formed a double-well trapping potential by focusing a sheet of light into the cloverleaf trap to repel atoms from the centre. Evaporation then produced two separate condensates. These were allowed to free-fall under gravity and expand ballistically.
After dropping 1 cm the clouds overlapped horizontally and the interference pattern was observed by absorption (figure 6). The period of the fringes is 15 p.m, which agrees with the estimated relative de Broglie wavelengths of the overlapping clouds. When the resolving power of the imaging system is taken into account, the intensity difference between the light and dark fringes implies that the modulation of the atomic interference was between 50% and 100%. An exciting feature of figure 6 is that it is a real-time photograph of interference. In traditional experiments that have demonstrated the wave nature of matter, the wavefront of a single particle is split and then recombined, and this is repeated many times to build up an interference pattern.
High-contrast interference was also observed between two pulses of atoms extracted from a double condensate using the radio-frequency output coupler. This demonstrates that it is possible to extract a coherent beam of atoms from a Bose condensate, and is a rudimentary realization of an atom laser.
Where do we go next?
Bose-Einstein condensation has not only provided us with a novel form of quantum matter, but also a unique source of ultracold atoms. Evaporative cooling has made nanokelvin temperatures accessible to experimenters, and with further optimization it should be possible to produce condensates of 108 atoms in timescales of 5-10 seconds. This production rate is comparable to the performance of a standard light trap, and indicates the potential for Bose condensation to replace the magneto-optical trap as the standard bright source of ultracold atoms for precision experiments and matter-wave interferometry.
The experiments to date have studied some of the basic properties of condensation, and have found good agreement with theory. The observation of phase coherence in BEC is a significant step that has opened the door to work with coherent atomic beams. However, a number of fundamental questions that can be addressed by experiments still remain, in particular with regard to the dynamics of Bose gases, such as the formation of vortices and superfluidity.
Another important direction is to explore other atomic systems. The work at Rice with lithium has made the first steps towards understanding Bose gases with negative scattering lengths. Recently at Boulder two different types of condensate were produced in the same trap by “sympathetic cooling”. In this scheme a cloud of rubidium atoms in one energy state was cooled in the usual way with evaporation, while a second cloud of atoms in a different energy state was simultaneously cooled just by thermal contact with the first cloud. Such cooling of one species by another will make ultracold temperatures accessible for atoms that are not well suited to evaporation, such as fermionic atoms whose elastic scattering rate vanishes at low temperatures, or rare isotopes that can only be trapped in small numbers. Fermions do not condense but cooling them into the regime where quantum statistics applies could yield valuable insights into Cooper pairing and superconductivity.
It is always exciting when subfields of physics overlap. Atomic physics has traditionally dealt with individual atoms or interactions between a few atoms. The realization of BEC in dilute atomic gases now allows us to study many-body physics and quantum statistical effects with the precision of atomic physics experiments, and it is exciting to see the rapid progress that is being made in exploring these new quantum gases.
Further reading
Observations of BEC
M H Anderson et al. 1995 Observation of Bose-Einstein condensation in a dilute atomic vapor Science 269 198
M R Andrews et al. 1997 Observation of interference between two Bose condensates Science 275 637
C C Bradley et al. 1995 Evidence for Bose-Einstein condensation in an atomic gas with attractive interactions Phys. Rev. Lett. 75 1687
K B Davis et al. 1995 Bose-Einstein condensation in a gas of sodium atoms Phys. Rev. Lett. 75 3969
J R Ensher et al. 1996 Bose-Einstein condensation in a dilute gas: measurement of energy and ground-state occupation Phys. Rev. Lett. 77 4984
W Ketterle et al. 1996 Bose-Einstein condensation of ultracold atomic gases Physica Scripta T66 31-37
Theory
F Dalfovo and S Stringari 1996 Bosons in anisotropic traps: ground state and vortices Phys. Rev. A 53 2477
S Giorgini, L Pitaevskii and S Stringari 1996 Condensate fraction and critical temperature of a trapped interacting Bose gas Phys. Rev. A 54 R4633
S Stringari 1996 Collective excitations of a trapped Bose-condensed gas Phys. Rev. Lett. 77 2350
Superfluidity
R Donnelly 1997 Rotons: a low-temperature puzzle Physics World February pp25-30