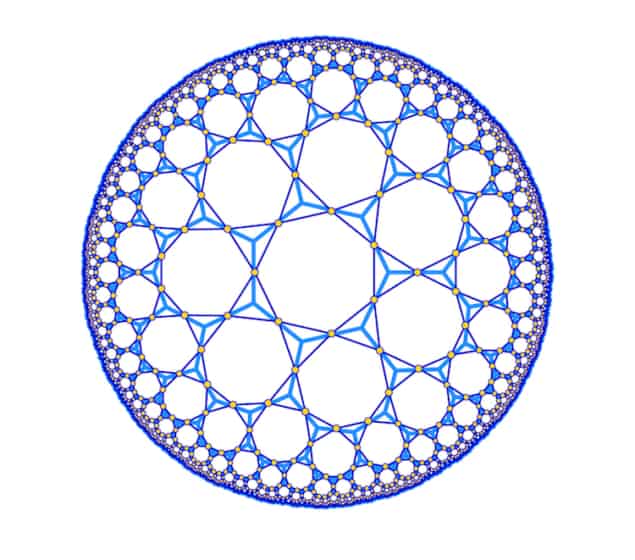
Building on previous work that realized Euclidean lattice models using circuit quantum electrodynamics (QED) and interconnected networks of superconducting microwave resonators, researchers at Princeton University and the University of Maryland have now made a coplanar waveguide array in which photons move as if they are in hyperbolic, negatively-curved, space.
Euclidean geometry describes the flat space of the non-relativistic physics world. It can describe Newtonian gravity, but it fails to describe gravitational radiation or strong gravitational fields that require general relativity in which gravity appears as a curvature of space-time. Non-Euclidean geometry is obviously difficult to study because of the, literally, astronomical distances involved so physicists are trying to reproduce it in experiments in the laboratory.
The most intuitive way to consider curved space is to think about the behaviour of straight lines in this space. In flat Euclidean space, two parallel lines are always a constant distance apart. In positive curvature, parallel lines converge. Negative, or hyperbolic curvature is more difficult to imagine, however, since the lines diverge. The resulting scale is thus much bigger than in flat space.
Although positive spatial curvature is easy to realize – it can be represented by the surface of a sphere – negative curvature is more difficult because it cannot be easily reproduced in our Euclidean world without distorting the physical system in which it is being studied.
Previous attempts to do this have involved hyperbolic metamaterials in which the dielectric constant is varied to reproduce the effects of negative curvature, but such experiments are purely classical. Researchers have also managed to make analogues of event horizons and Hawking radiation using acoustic waves, ultrashort optical pulses and Bose-Einstein condensates. They have even put forward techniques to realize the Dirac equation in curved space-time by using ion traps, optical waveguides and optical lattices with so-called non-Abelian artificial gauge fields.
Cavity QED
Researchers have been studying cavity QED with superconducting circuits for 20 years now. Here, they use lattices of coplanar waveguide resonators as artificial materials for microwave photons whose interactions they can then study either by directly using nonlinear resonator materials or by coupling them to superconducting qubits.
The Princeton and Maryland team has now exploited a previously overlooked property of such resonators: that they are highly unique lattice sites that can be deformed without changing their properties.
A coplanar waveguide is a 2D analogue of a coaxial cable and consists of a central conductor surrounded by a dielectric gap. The researchers made a resonator from this waveguide by cutting the end of the cable, which then forces microwaves to bounce back and forth off the ends and form standing wave modes.
“Like a coaxial cable, the waveguide can be stretched out or coiled up without changing its total length,” explains team leader Alicia Kollár. “This allows us to make lattice sites that are identical from the point of view of the solid-state physics we wish to study, but occupy different-shaped regions on the device and connect differently to their neighbours.
“This flexibility allows us to produce lattice models that would otherwise be impossible.
“An analogy I like to make here is a football with a large atom at the centre of every patch (essentially the configuration of C60 buckminsterfullerene). Now, even if you cut the football in half, there is no way to get it to lie flat without tearing or stretching it. What we can do with coplanar waveguide resonators, however, is to stretch a structure without changing the physics.”
Unique table-top experiment
The result is a device that is 2D, planar and Euclidean, but which has the physics of non-Euclidean geometry, she tells Physics World. The example described above is the case of spherical (positive) curvature, but it can also be realized for negative curvature.
“This device provides us with a unique table-top experiment in which to produce hyperbolic geometry,” she says. As well as being useful for studying general relativity, hyperbolic lattices are also important in mathematics – for example to study non-commutative groups, graph theory and random walks. Computer scientists also study hyperbolic networks since they can be used for robust and efficient communication. Indeed, the connectivity of the Internet is a hyperbolic map.
Heptagon kagome
Because of some technicalities of these resonators, the easiest lattice to form is a “kagome” lattice (named after a Japanese basket-weaving technique), she explains. This lattice is characterised by six-pointed stars (hexagons surrounded by equilateral triangles). “Curved-space versions of this lattice occur if we use pentagon and five-pointed stars or heptagons and seven-pointed stars instead of hexagons and six-pointed stars.”
Quantum spin liquid state pathway emerges
The researchers say they chose to make the heptagon kagome in their work because, as well as being curved, it also boasts another highly unique feature: a large fraction of degenerate states completely separated from all the other eigenstates of the lattice. “Such a feature is known as a flat band and in solid-state physics is known to give rise to many-body physics phenomena,” says Kollár. “There are, however, only a very few naturally-occurring cases (and some theoretically known ones) in which this flat band occurs by itself, rather than in the immediate vicinity of a more conventional band.”
In follow-up to this work, the team has already started looking into how to maximize the gap surrounding the flat band to optimize experimental performance.
“We would now also like to incorporate qubits and non-linearity into our coplanar waveguide,” reveals Kollár. “The device discussed in the present work contains only linear resonators, but by adding qubits we can start to introduce effective photon-photon interactions and engineer photon-mediated spin models.”
The research is detailed in Nature 10.1038/s41586-019-1348-3.



